This is How a Hopfield Network Learns to Let Go (Technically Speaking)

The code behind moving on: Hebbian learning & weight matrices explained

I’ve been putting this post off for a while now. Because how do I explain something as convoluted as code and math in a way that makes it digestible to those who aren’t in its orbit? Let alone those who don’t even want to be?

I mean, I completely get it. These topics can be so obscure and abstract that they overwhelm me as well (not saying I’m a genius or anything).

So honestly? I’m not even sure myself….

Einstein once said, “If you can’t explain it simply, you don’t understand it well enough”.

And I completely agree. But it’s deeper than that for me.

Because in a way, these posts aren’t just explanations. They’re the physical evidence of how much this all means to me.

To be able to take something as complex and delicate as human memory, as computational learning, and ground it through lived metaphor. To translate convoluted theory into something people don’t just understand, but can actually feel and hold in themselves. (And yeah also, to have people not look at me like I’m crazy of course).

That is everything to me.

These words, these models, these analogies.

They’re my attempt to show the world why I love this field so deeply. Why it’s my resonance. Even if the world doesn’t fully understand. Even if it’s too visceral, too theoretical, too abstract.

This is what memory means to me.

What it feels like to study it. To live it. To get frustrated by it. To model it. To try to understand it.

So, let’s get started. Let’s see if I can make you romanticize math.

---

How Hebbian Learning Enables Hopfield Networks to Simulate Your Heartbreak (Continued..)

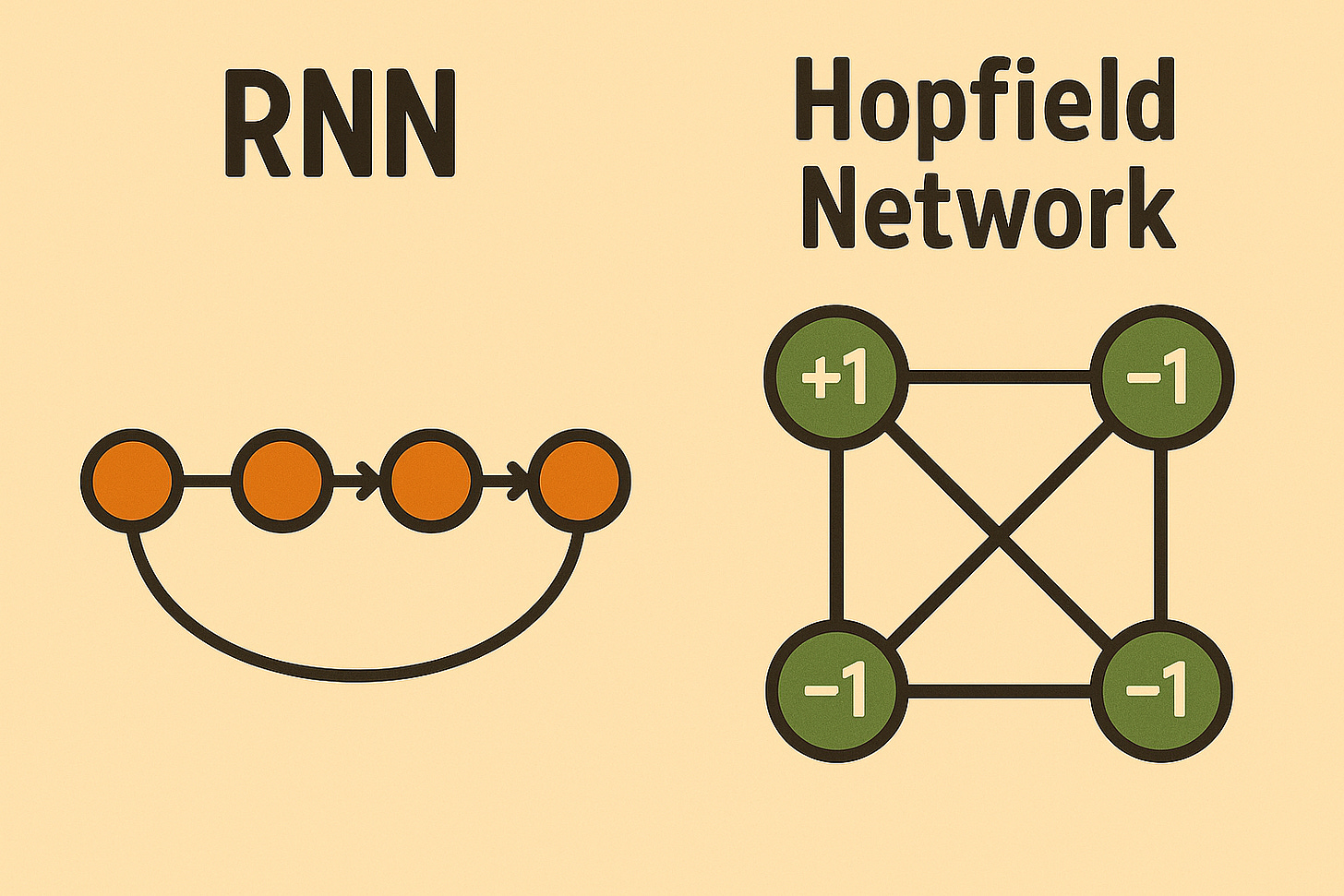
Hopfield networks are a special type of recurrent neural network (RNN) that embody the principles of dynamical systems theory. Traditional RNN models process inputs sequentially, learning to predict what’s next in a sequence. But because of that dynamical systems edge, Hopfield models function a bit differently.

Instead of predicting, inputs settle into stable attractor states through Hebbian learning. Each neuron’s state influences the others. Through iterative updates, the network converges to the most stable, energy-efficient arrangement (cue: all our previous examples).

So, while most RNNs are viewed through the lens of prediction, Hopfield networks are analyzed through the lens of energy minimization and stability.

Hopfield neurons are binary i.e. there are only 2 possible states for each neuron (wave function collapse much?):

• +1 (on / white)

• -1 (off / black)

While this may be a simplification of how memory works, it's actually intentional. The idea here is that memory can be represented with discrete, binary values to create stable attractors in a dynamical system. (The update rule also relies on this binary formatting to determine which neurons turn on/off when recalling a pattern but more on that later).

To work with this computationally, we must preprocess images into vectors of +1/-1. This is why we grayscale images beforehand. By reducing images to a single channel (instead of three for RGB/colored images), we can then implement a threshold to binarize the pixels.

def preprocess_image(path, size=32): 
    ''' 
    Resize to fixed size (32x32),
    Convert to grayscale (L = grayscale),
    Binarize (white=+1, black=-1),
    Flatten to 1D vector 
    '''
    
    img = Image.open(path).convert('L')  
    img = img.resize((size, size))

    img_array = np.array(img)

    # binarize pixels where > 127 is +1, else -1 (threshold)
    binary_array = np.where(img_array > 127, 1, -1)

    return binary_array.flatten()

This transforms the image to a symbolic structure of what is or isn’t present in the pattern. It only keeps what's essential for pattern recognition.

And because every neuron in a Hopfield network is fully connected to each other, we flatten the 2D image into a 1D vector, so that each pixel becomes a neuron in the network (e.g. an image size of 32x32 means a vector of 1024 values or 1024 neurons in the network).

This is how a computational model becomes a framework to understanding ourselves.

Now that we’ve compressed these images, we can train our network to learn the patterns. Memory encoding is how we embed these patterns into our computational-network-of-a-brain.

# MEMORY ENCODING
def train_hopfield(patterns, repeats=1):
    '''
    Train network via Hebbian learning!
    W = sum(outer products of each pattern with itself)
    '''

    n = len(next(iter(patterns)))  
    W = np.zeros((n, n))

    for i in range(repeats):
        for pattern in patterns:
            W += np.outer(pattern, pattern) # HEBBIAN LEARNING

    np.fill_diagonal(W, 0)  # prevents self-connections
    W /= len(patterns)

    return W

Weight matrices provide the symmetrical structure that underlies how neural networks learn (consider them as the model’s brain). Hopfields are no different in that sense. But what makes them unique is how they learn.

Hopfield networks build their weight matrices W via Hebbian learning.

“Neurons that fire together, wire together”.

But what does that even mean?

When we feed the network a binarized, flattened image pattern (our 1024 neuron vector), the network encodes the relationship between each pixel pair. Hebbian learning determines which neurons are +1 (on) or -1 (off) in the pattern. The outer product of the pattern with itself provides the complete wiring of its internal structure (essentially, it shows how each neuron influences the other based on its activations). And by summing across all the patterns, we embed those associations into its memory.

Together, this is how the matrix shapes the network’s landscape. Each learned pattern becomes an attractor the system comes home to during recall.

During pattern retrieval, our network completes “incomplete” and “noisy” memories i.e. why your brain still recalls your ex even though it's over (yikes).

What’s happening is that your Hopfield brain learned to associate that your ex was the complete memory for A LOT of things. So now, even the smallest fragment feels “incomplete” without him. Like something is missing (double yikes...).

I'm giggling to myself now because I'm thinking of a 15 year old girl crying, “...but he was my world!”. And honestly? You're not not valid. Your brain just learned to associate “your world” with him from all that time. It built the attractor.

Hopfield networks do this too.

They rely on their trained weight matrix W, which encodes all the associations they’ve learned, to pattern complete and fill in “what's missing”.

# PATTERN RECALL 
def recall_pattern(W, pattern, steps=10, tolerance=0):

    '''
    Provide "incomplete/noisy" input,
    Model iteratively updates via weight matrix,
    Settles into a memory attractor state
    '''

    state = pattern.copy()

    for i in range(steps):
        new_state = np.sign(W @ state) # UPDATE RULE
        new_state[new_state == 0] = 1  # avoids zeros states
        if np.array_equal(new_state,state):
            return state, i # converged in i steps
        state = new_state

    return state, steps

This is how the update rule works. When given an input that seems incomplete, the network will iteratively go through its weight matrix (e.g. 10 steps here) to converge to the most familiar memory it knows. It transforms the current state to the most stable, low energy attractor.

But that doesn't mean that the outcome is always correct. It just means that it’s what’s been most reinforced.

The attractor isn’t about truth, it’s about learned associations.

Okay so clearly, we need to retrain the system to understand that not everything is associated with the ex.

To do this, we're going to create new patterns i.e. new memories without him (finally...).

But, the original weight matrix W, the one that made him the baseline, isn't going to be deleted or thrown out because that's just not how memory works.

# REINFORCEMENT 

def reinforce_memory(W, new_pattern, repeats=1):
    '''
    Reinforces new memory patterns WITHOUT erasing the past
    Simulates how human brains strengthen new associations over time
    without deleting the past (bc that's not possible)
    '''

    for _ in range(repeats):
        W += np.outer(new_pattern, new_pattern)
    np.fill_diagonal(W, 0) # no self-connections


    return W

The old memories will still be there. But as we introduce new patterns and reinforce new associations, our network will shift over time. And those memories? The weight of those old associations? They can echo, but they’ll no longer define you. They'll fade into the background. Your system reshapes.

So, how does this happen computationally? We update the initial weight matrix by giving it new patterns to learn through reinforcement.

W_temp = W_base.copy()

scene_names = ['beach', 'christmas', 'movie', 'night', 'surf', 'brunch', 'picnic']

for repeats in range(1, 31):
    bg = random.choice(bg_keys) # random selection
    scene = bg.replace('_bg', '')

    # scene patterns
    bg_input = memory_dict[bg]
    noisy_bg = add_noise(bg_input, amount=0.1) # add noise to input
    benji_key = bg.replace('_bg','_benji')
    ex_key = bg.replace('_bg','_ex')
    benji_pattern = memory_dict[benji_key]
    ex_pattern = memory_dict[ex_key]

    # reinforce benji
    W_temp = reinforce_memory(W_temp,
                            new_pattern=benji_pattern,
                            repeats=1) 

    # recall via noisy bg
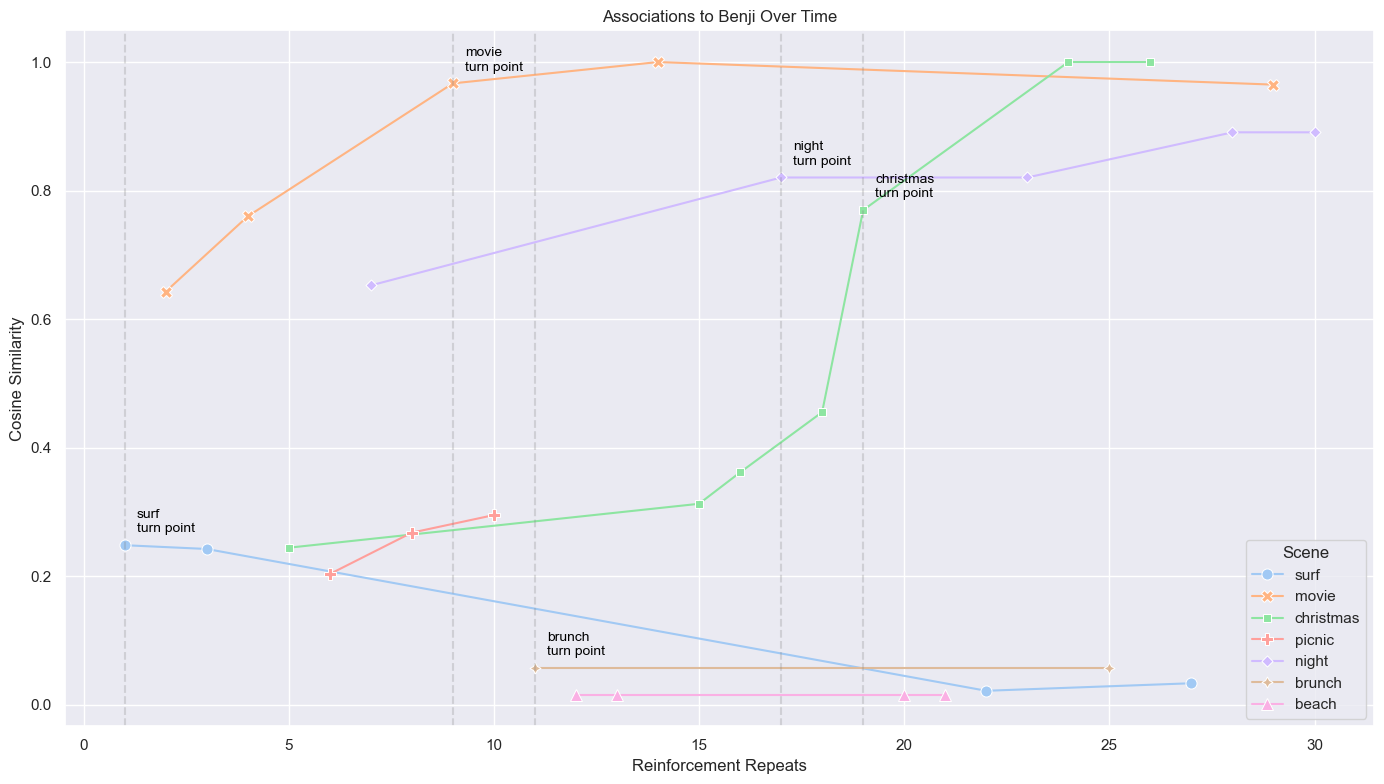
    recalled, steps = recall_pattern(W_temp, pattern=noisy_bg)

For the seven different cartoon scenarios I created, I ran the model for 30 reinforcements, randomly choosing a scene each time. That means not every memory had the same amount of repetition. And that’s intentional.

I added noise to the input to simulate reality. Emotional distortion, faded cues, imperfect recall. How strong is the memory association? If someone mentions just color not even specifically blue, will you think of your ex? I forced the system to remember under messy conditions, just like how we are.

This specific “night” scene had a total five reinforcements. And by its second iteration? The attractor had already started to shift.

In the graph below, cosine similarity was used to calculate the model’s ability to recall the new association (i.e. the cartoon dog based on my real dog, Benji) instead of the ex association for each reinforcement run.

Now the turning point? That’s what we want. That’s when the model first recalls the new association instead of the ex. The first break in the system.

Some scenes switched early on, but then decayed (surf). Others took a bit longer, but eventually stabilized (Christmas). And few, never even had a turning point (beach).

Some associations may linger, not because of emotional weight. Simply because they were encoded earlier, deeper, or more often. Memory persistence isn’t always about meaning. Sometimes, it’s just history.

Why didn’t I reinforce each scene equally? Because that’s not realistic, is it? Healing doesn’t happen like that. Every day is already a day without him. New associations affect the matrix as a whole (everything is summed together). Even if a pattern isn’t often reinforced, it still shifts the network subtly. It might not be dominant, but it’s still part of the system.

Valentine’s Day only comes once a year. And while you may remember he was your Valentine’s last year, you don’t need to relive that day 30 times without him to move on.

What I’m trying to say is that, some memories fade more easily because of frequent exposure. Others may linger because of circumstances. And that’s okay.

Because these memories are all a part of you. It’s a part of your past. They don’t get erased. What’s really important is that over time, the attractor states that were initially him? Will shift.

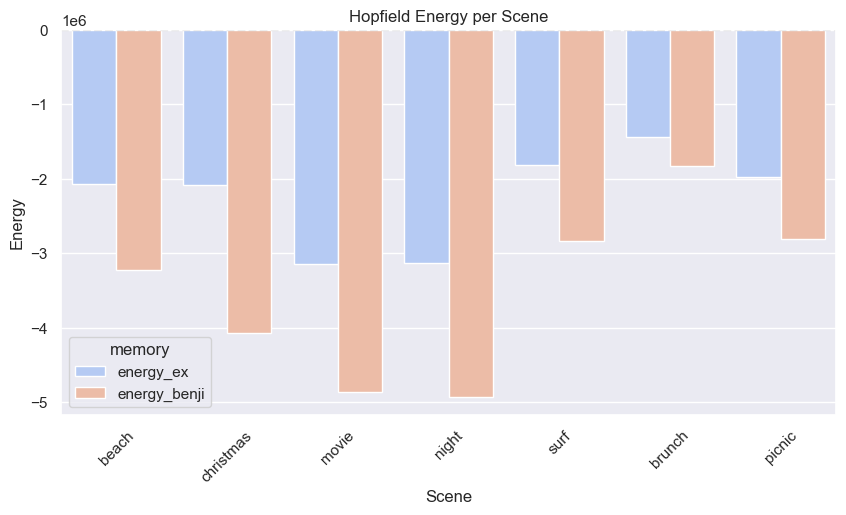
Think of energy as the depth of a memory basin. The lower the energy, the more stable the memory. The graph below shows the energy for each scene, comparing the ex basin to the Benji basin. Notice how in every case, Benji’s basin is deeper. This is the system creating new stability over time.

We don’t need to delete memories. We don’t need to pretend your ex never existed. We just need the emotional basin holding your attachment for the past to get shallower. Through the initial system destabilization. Through reinforcement. You’re now slowly reshaping your landscape. And so is the model.

---